
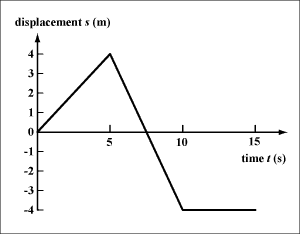
It is travelling at a ''''constant velocity'''' of ''''-2.7ms^-1^'''' back to its starting point, our reference point 0.
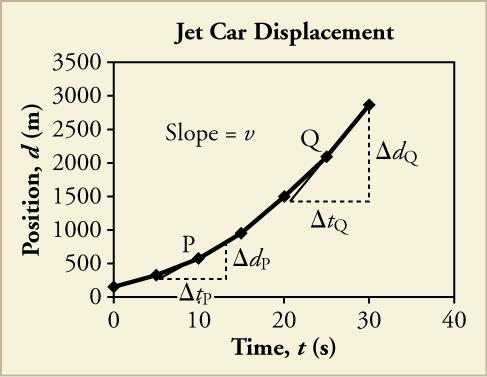
It is '''stationary for 3 seconds'''ĭuring ''''Part C'''' of the journey the object travels '''-8m''' in '''3s'''. It is travelling at a '''constant velocity''' of '''+2ms^-1^'''ĭuring ''''Part B'''' of the journey the object travels '''0m''' in '''3s'''. For instance.ĭuring ''''Part A'''' of the journey the object travels '''+8m''' in '''4s'''. When describing the motion of an object try to be as detailed as possible. In Physics, we specify the origin landmark at 0 and the points either side of it are either positive or negative numbers (in units of metres). Now left or right is not a good distinction as not everyone can agree with it. 5 metres from the door does not mean anything without giving some indication of direction (inside or out for example). Along a straight line, you only need the position of the landmark and how far the object is from the landmark left or right (or east or west). To describe the position of a moving object, you have to specify its position relative to a particular point or landmark that is understood by everyone. Will two cars crash if they are heading towards each other as they apply brakes at a certain time? In most mechanical problems we are asked to determine the connection between speed, position and time. This cannot be shown on a distance-time graph. Usually, a line with a negative gradient would indicate motion going backwards. Its distance would be the total length of the journey.Ī displacement-time graph is able to show if an object is going backwards or forwards. If an object goes back to where is started in certain time, then its displacement is zero. ''''Displacement'''' is the length between start and stop positions and includes a direction. Therefore '''Δt''' means '''"change in time"''' The '''Δ''' is just short hand for '''"change in"'''. You may also notice that the formula for calculating speed is sometime written with small triangles '''Δ''' (the Greek letter delta) in front of '''d''' (distance) and '''t''' (time). You can even do this for a curved line where the speed is changing, just remember that your result is the '''average''' speed in this case. The average speed can be calculated for any part of a journey by taking the change in '''distance''' and dividing by the change in '''time''' for that part of the journey. =Calculating Speed from a Distance-Time Graph= You can see that the distanced moved through each second is changing. The object is either getting faster = ''''accelerating'''' or slowing down = ''''decelerating''''. ''''Curved lines'''' on a distance time graph indicate that the speed is changing. A moving object is always ''''increasing'''' its total length moved with time. On a distance-time graph, there are no line sloping downwards. Note that you can think of a stationary object (not moving) as travelling at a constant speed of 0 m/s. ''''Straight lines'''' on a distance-time graph tell us that the object is travelling at a '''constant speed'''.
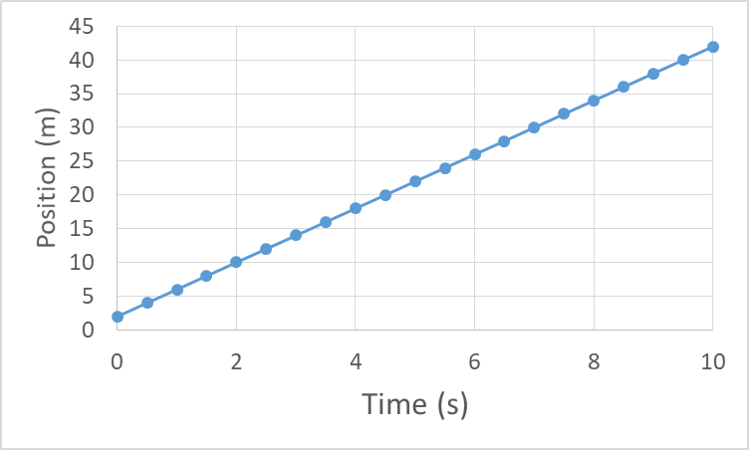
The standard unit is the ''''metre''''.Ī distance-time graph shows how far an object has travelled in a given time.ĭistance is plotted on the Y-axis (left) and Time is plotted on the X-axis (bottom).īelow you can see that the object represented by the blue line has travelled 10m in 2s whereas the object represented by the red line has only travelled 4m in this time and is therefore travelling more slowly. ''''Distance'''' is the total length travelled by an object.


 0 kommentar(er)
0 kommentar(er)
